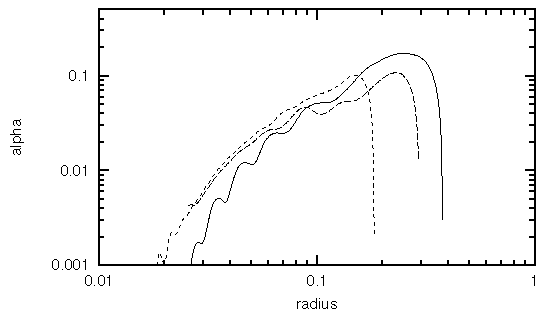
STANDARD MODEL
Our standard model has a sound speed of 0.25, a mass ratio of unity,
and an initially flat density profile. The Mach number of the
rotational flow is of order 12 in the interior of the disk. A
two-armed spiral shock quickly develops, and remains relatively steady
for a few binary orbits. This evolution is best seen in the
animation of this simulation.
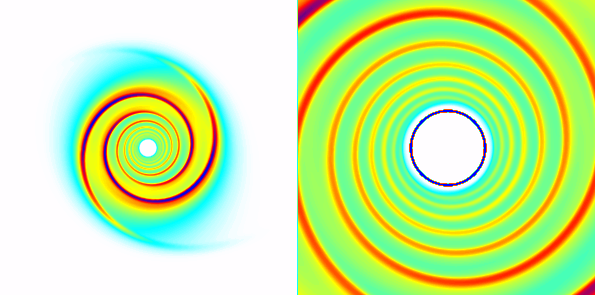
The left image shown below is of the entire numerical grid, with the
binary companion oriented to the right of the disk. The image on
the right is an expanded view (a factor of 5). The inner circle is
the inner boundary of the numerical grid, at a radius of 0.02.
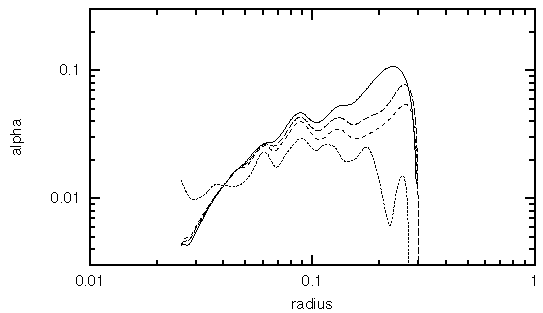
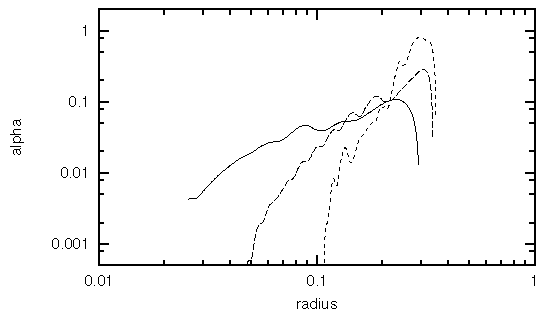
The evolution of the mass transport during the simulation is illustrated
below. The first three lines are from the first few orbital periods, when
the double spiral pattern dominated the disk. The dotted line is from
the end of the simulation, when other wave modes are interacting with the
double spiral.
DEPENDENCE ON MACH NUMBER
We ran additional simulations with colder disks, since CV systems are
characterized by relatively high Mach number. Colder disks have
more tightly-wound spiral waves that decay faster with decreasing
radii. In our coldest disk with an internal Mach number of order 40,
the double spiral is gone inside a radius of about 0.1. In its place, one
can see a single-armed spiral wave, but this too decays away before
reaching the inner radius of the disk. Colder
disks are also more unsteady, as seen in the
animation. The figure below shows disks
with sound speeds of 0.25, 0.125, and 0.0625.
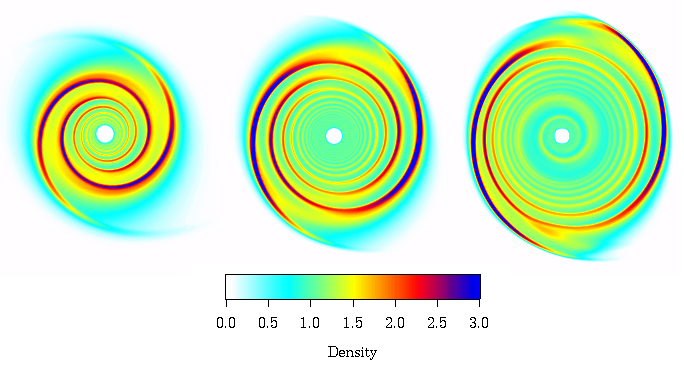
The effective alpha, however, is still of order 0.1 in the outer regions
of the accretion disk, where the double spiral is relatively strong.
DEPENDENCE ON MASS RATIO
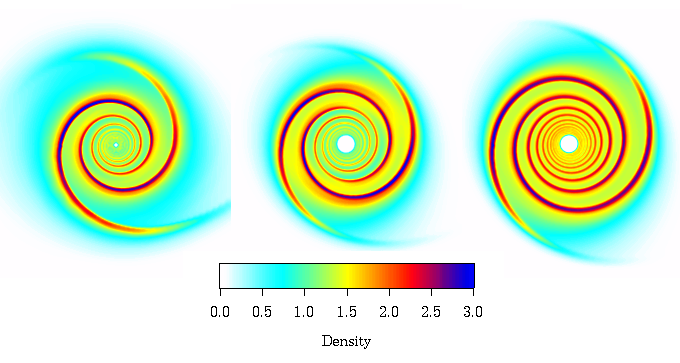
We ran additional simulations with smaller (q=0.2, on the left)
and larger (q=5, on the right)
mass ratios. The strength of the spiral waves was relatively constant
in all of these models.
The effective alpha is relatively independent of mass ratio. The
only significant difference between these models is the location
of the outer disk edge, as determined by tidal truncation.