The data reduction of UV data is roughly made of two main steps: reduction
of UV files, output of which are dirty maps, and reductions of dirty maps,
which contain a big amount of noise which results from diffraction and sidelobes
of antennas. Making dirty maps is fairly easy ( at least judging from what *I* know).
For that(and all the other things) we use the software called AIPS, which is written
on Fortran. There is a bunch of commands which can be used in order to make dirty
maps--horus, mx, etc. Here is the dirty map of 3c397 in C band.
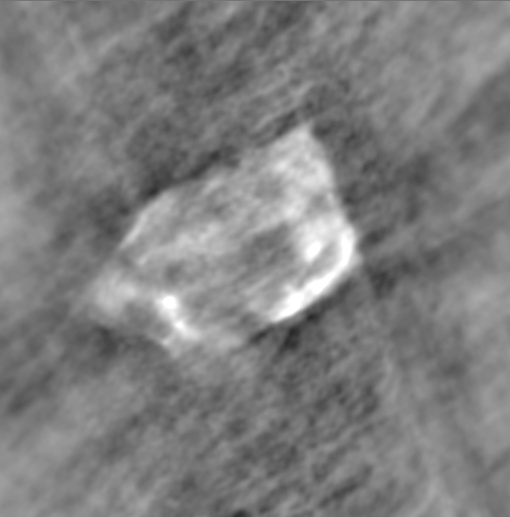
In order to be precise I have to say that this is the map of Intensity(which
is represented by Stoke's I parameter).
The next step of the reduction is the cleaning of our map. For that we can
use mx, clean, or other "subprograms." However, before begining to cleanse the
map, we have to figure out how much of noise is over there, in order not to
"overclean" the map, erasing some parts of possible sources. Thus, before
passing to this step, we have to do some preliminary data inspection, which will
result in us knowing how much of noise is there in the data. The following picture is
the Intensity vs. #pixels plot for a rectangle in the previous dirty map.
The recangle was chosen so that the obvious part of the source is not included in it.
The plot(called histogram) shows how many pixels of a particular intensity are
there in the box.
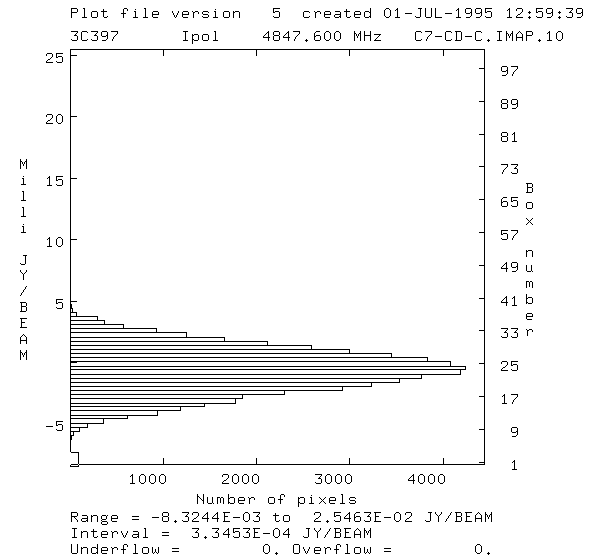
As you can see, here we have a Gaussian centered at zero. This is exactly what we should
expect: a territory filled with values which average to zero --a characteristic of
noise. Thus, we can say that the box was accutaly filled with noise.
As we can see, there is a huge amount of noise in this map. To see better where does
this amount of dirt comes from,
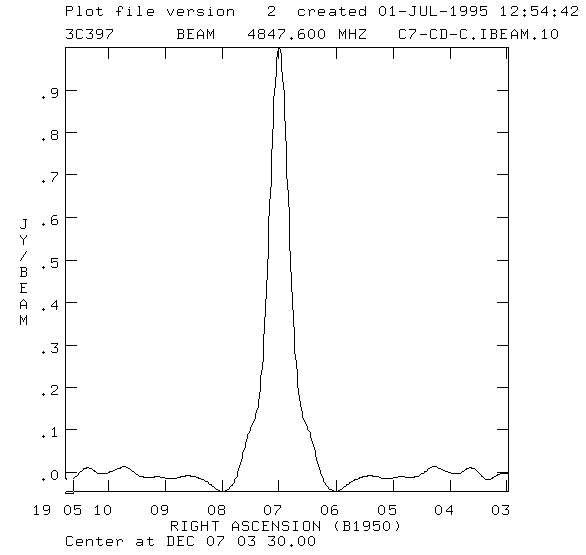
here is the immage of the synthesized beam of the whole VLA.
The ideal case would be a dot in the middle of the picture. However, because
of diffraction effects(which constitute the sidelobes of the antenas), we rather
have a dot with lines that pass through it. Another way to understand this
map(at least as much as I understood it) is to say that it is what the observer on
the supernova sees when he looks on the antena array. Here is the plot of
the intensity vs. distance for a line which passes through the middle of our beam.
This reminds me the intensity pattern of a single source...or rather a source made
of very closely spaced little sources(however, I still need to make sure
that this way of understanding is correct, so have patience).
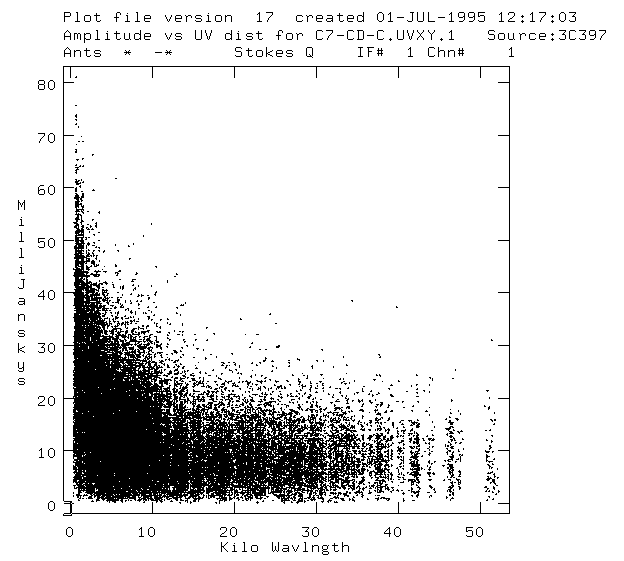
As already said, before cleaning the map, we first need to find an idea about the
noise, and also it would be usefull to have some ideas about the sky coverage of
the array. Here is the plot of Intensity vs. the baseline for different
pairs of antenas. The baseline is measured in wavelengths, and is the distance
between the lines of vews of the two antenas(which make the pair, and there
are actually more than 300 pairs). As we see, bigger the baseline is, smaller
is the intensity.
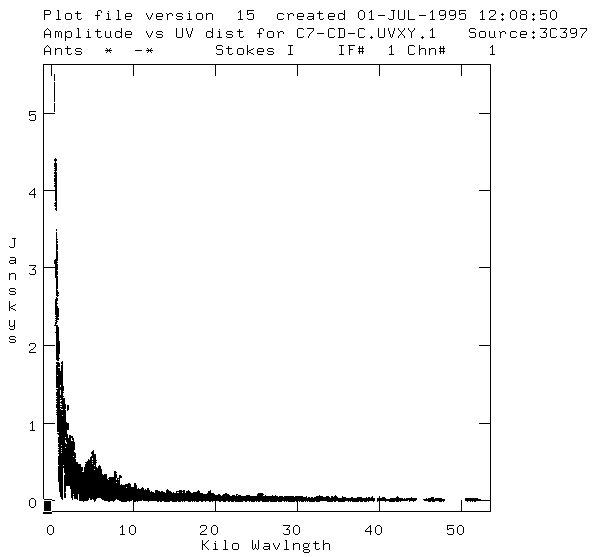
The previous and next two plots are those of Intensity versus
baseline(the distance between two antenas' beams, which are parallel, of course).
As we see, there is bigger reponse for smaller baselines, which is normal:
the combination of two closely spaced antenas "sees" a much bigger angle
without interference. If you are being more observant, you will see some
"wild" points, which deviate from the average plot, and which obviouselly
correspond to some "wild" effects which give false data. So what we do
is that we go and delete the data assosiated with those "wild" points.
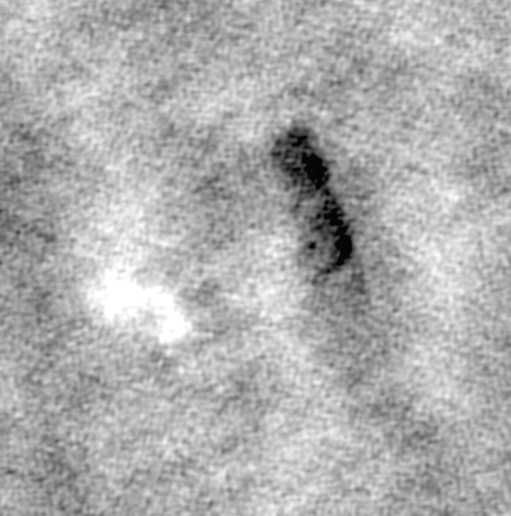
Next is the map of circular polarization. As you can see, it is completely
made of noise--which is exactly what we extpected: the emmission from
cynchrotron radiation that we can see from a supernova is only
linear(because of some primitive reasons). The reason that we see some
black(negative) pattern on one side, and a symmetrical white pattern,
comes from the "beam squint." What is a beam squint? The thing is that
the linear polarization can be brocken into the sum of right-handed and
left-handed circular polarizations. Thus, at the base of the antena
there are two VERY closely spaced reseptors of circular polarization(one
of the measures the right-sided, the other one--the left-sided.) Their
signals are being added. Had that "VERY" been zero, we would record
linear pol. only. However that "VERY" is finitely close to zero, and as
we deviate to the sides, the signal from one of the reseptors becomes
slightly biger than that of the other one. Thus we end up recording
some eroneous circular polarization.
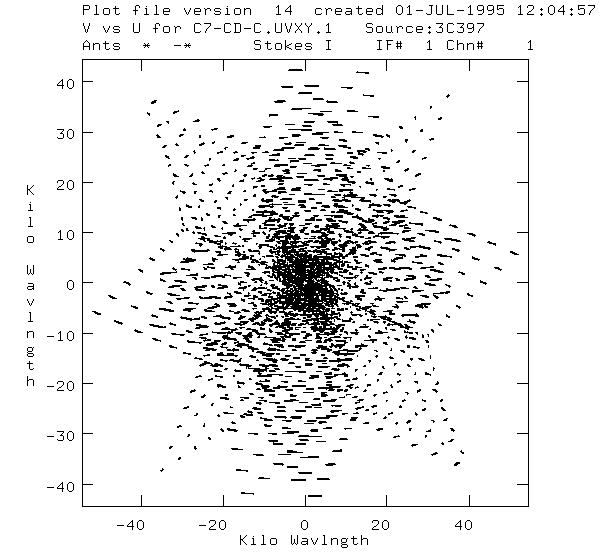
The next one is the plot of UV coverage of the array.
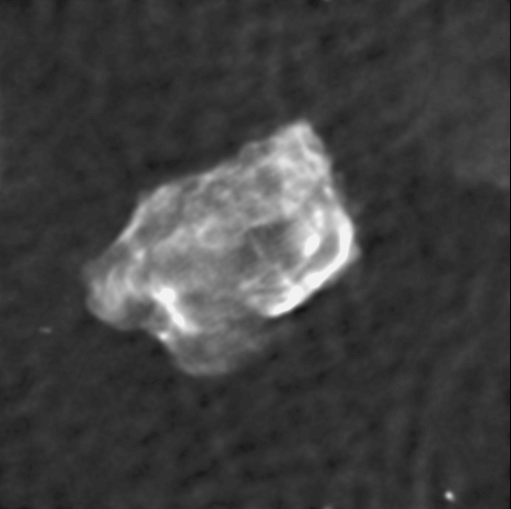
Here is the cleaned(with CLEAN algorithm) radio immage of 3c397 in L band.
As you can see, it still has some noise, which, however, is greately
reduced.
And here are the equivalent cleaned pictures in pseudocolors, in L band and
C band:
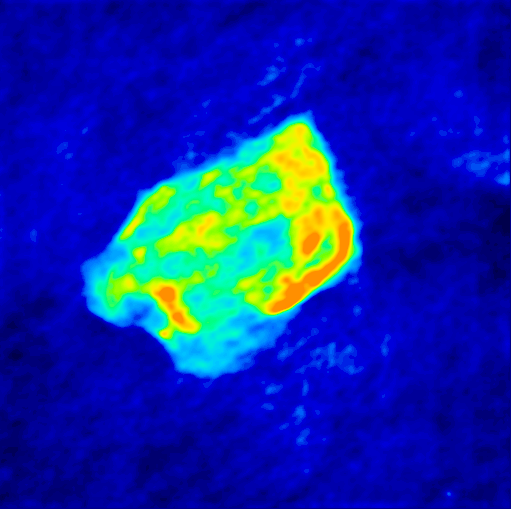
The immage of 3c397 in L band, made with CLEAN algorithm.
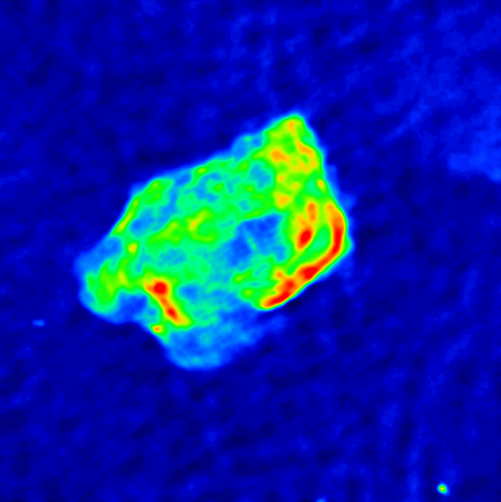
This is again in L band, but made with VITESS algorithm.
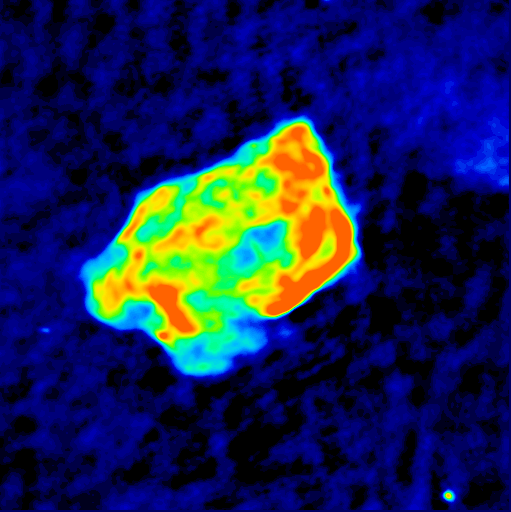
This one is in C band, made with CLEAN.
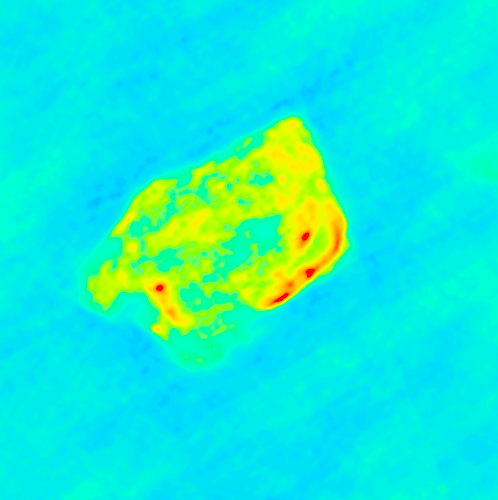
The same as above, made with VITESS.
