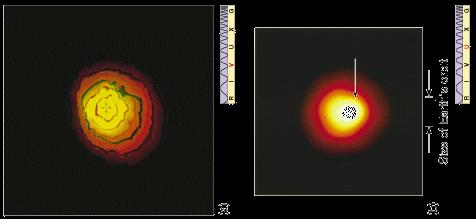
Betelgeuse
We can measure the radius of the Sun by measuring its angular
diameter (1/2 degree) and the distance to the Sun (150,000,000 km).
If the Sun were at the distance of the nearest star, 300,000 times
farther away, it would have an angular size 300,000 times smaller:
0.006". This is much smaller than the blurring of star images by
our atmosphere (1") and even smaller than the star images made
by Hubble (0.1"). So we cannot directly measure the radii of
most stars.
Some stars are big enough that telescopes can measure their
diameter directly.

Betelgeuse
For other stars we turn to physics...
We find that stars radiate roughly like blackbody radiators. This is important because it means that we can use the theory for blackbody radiators to infer things about stars. I have already noted that one can use the shape of the observed continuum and the Wien Law to infer the surface temperature of a star. To infer the radii of stars, we can use what is known as the Stefan-Boltzmann law.
The Stefan-Boltzmann law tells you how much energy a blackbody radiator of a given temperature radiates per unit area of it surface (i.e., it tells you the flux of radiation which comes off the surface of a blackbody as a function of its temperature). We have that
Flux of energy = constant x Temperature ** 4
The constant = 0.000057 in centimeters-grams-seconds units. In this case, the units of energy are known as ergs where 1 erg = 0.0000001 Joules. An erg is roughly the kinetic energy of a slow-flying mosquito.
Example:
Simply take the ratio of the energy fluxes, i.e.,
Flux 1/Flux 2 = constant (4,000)**4 / constant (2,000)**4 = 16
The hotter object is 16 times (2**4 times) brighter than the fainter object.
Now, take a star of temperature T. How luminous will this star be? Since the star is roughly a blackbody radiator, it wil produce a flux of energy at its surface given by constant x T**4. To figure out the total energy radiated, one needs to figure out how many square centimeters (or meters) there are on the star's surface. This is straightforward for a spherical star. The surface area of a sphere is 4 pi R**2. Combining the above two relations, we have that
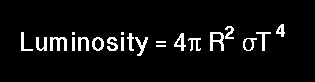
This simple relation allows reasonable estimates of stellar radii to be made.
Examples:
Well, we have that
10,000 L = 4 pi R**2 constant T**4
L = 4 pi r**2 constant T**4
So that
10,000 = R**2 / r**2 which implies that the more luminous star is 100 times larger than the fainter star.
L = 4 pi R**2 constant (6,000)**4
L = 4 pi r**2 constant (3,000)**4
and so
1 = R**2 / r**2 x 16
so that the hotter star is 1/4 the size of the cooler star!

